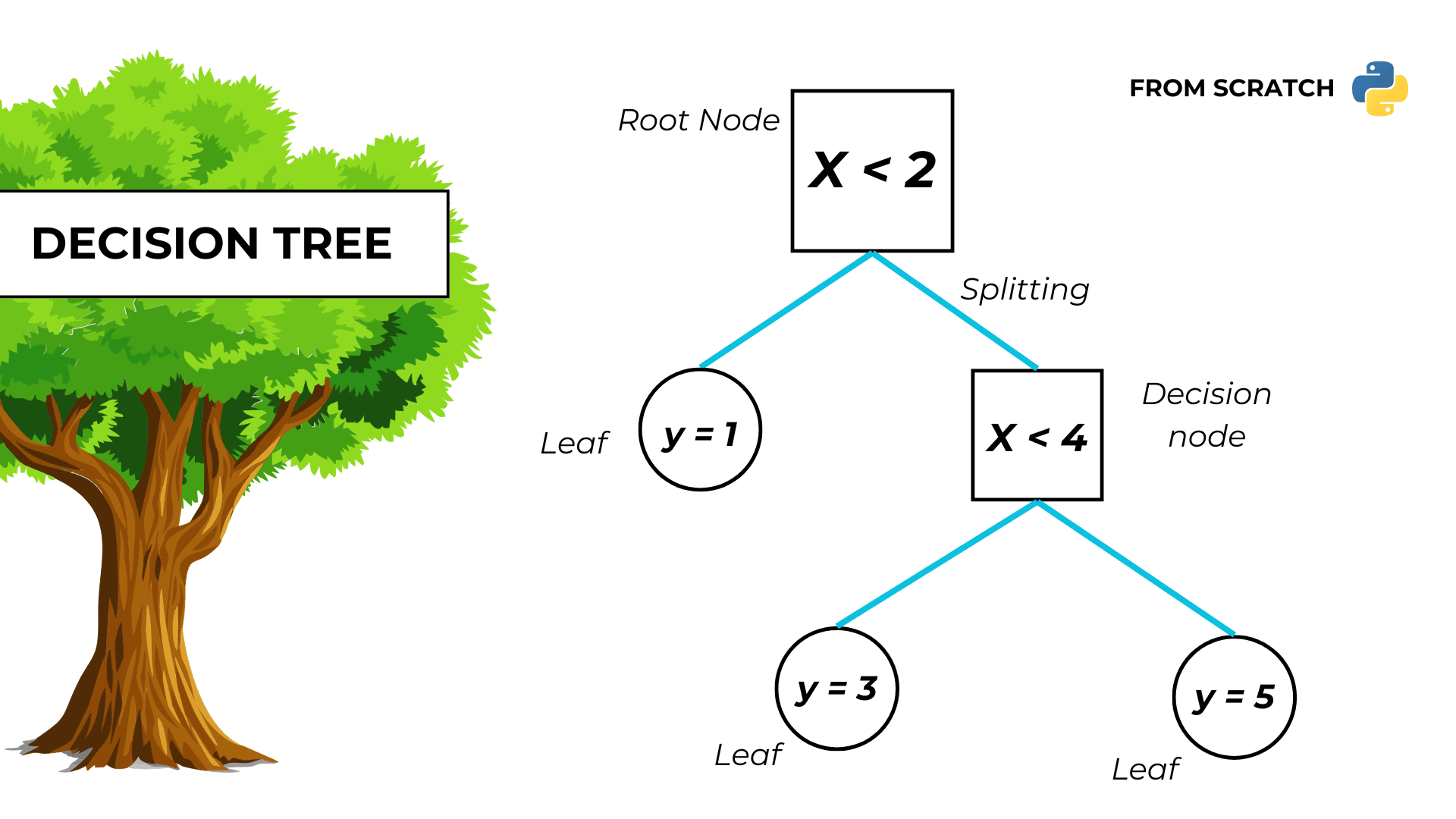
In this article, we’ll learn how to program a decision tree from scratch in Python using ONLY MATH.
Let’s get started.
Table of Contents
Why is building a decision tree from scratch useful?
When studying a new machine learning model, I always get lost between the formulas and the theory, and I don’t understand how the algorithm works.
And there is no better way to understand an algorithm than to write it from 0, without any help or starting point.
Disclaimer
I have already written an article that discusses decision tree thoroughly, explaining the mathematical concepts and steps of the algorithm with pictures and examples.
I suggest you read it before continuing.
Decision tree in Python
Problem statement
We want to solve a regression problem with only numerical features by fitting a decision tree to the data.
1. Import necessary libraries
import numpy
In this code I only use Numpy, a library useful for dealing with lists, to save space by computing the mean value of a list without iterating.
2. Define a dataset
X = {
"LotArea":[50, 70, 100],
"Quality":[8, 7.5, 9]
}
y = {
"SalePrice":[100, 105, 180]
}
This is a house price dataset with two input features: property area and quality of the materials; and one target feature: market price.
3. Define nodes
def create_node(datapoints):
datapoints = datapoints
mean_value = numpy.mean([train_y["SalePrice"][y] for y in datapoints])
mean_variance = numpy.mean([(train_y["SalePrice"][y] - mean_value) ** 2 for y in datapoints])
leaf = False if mean_variance != 0 else True
return {
# datapoints index in the node
"datapoints" : datapoints,
# mean output value of the data points in the node
"mean_value" : mean_value,
# impurity of the node
"mean_variance" : mean_variance,
# leaf state
"leaf" : leaf,
# best feature and treshold to split the node
"feature" : None,
"treshold" : None,
# the left sub-node of the node
"left" : None,
# the right sub-node of the node
"right" : None
}
The function create_node:
- Takes in input the indexes of the samples in the node and the training output dataset.
- Return a dictionary with the indexes and all of the properties of the node.
4. Define the split function
def split_node(train_X, train_y, node, feature, treshold):
node_left = create_node(train_y, [x for x in node["datapoints"] if train_X[feature][x] <= treshold])
node_right = create_node(train_y, [x for x in node["datapoints"] if train_X[feature][x] > treshold])
return node_left, node_right
The function split_node:
- Takes in input: training X, training y, the node we want to split, and the threshold.
- Create 2 nodes. Each data point in the node goes to the left if it is minor or equal to the threshold, and vice versa.
- Return the left and right nodes.
5. Find the best threshold for a node
def find_treshold(train_X, train_y, node):
values = []
impurities = []
for feature in train_X:
for treshold_index in node["datapoints"]:
node_left, node_right = split_node(train_X, train_y, node, feature, train_X[feature][treshold_index])
if len(node_left["datapoints"]) == 0 or len(node_right["datapoints"]) == 0:
continue
weighted_impurity = node_left["mean_variance"] * len(node_left["datapoints"]) / len(node["datapoints"]) + node_right["mean_variance"] * len(node_right["datapoints"]) / len(node["datapoints"])
values.append([feature, train_X[feature][treshold_index]])
impurities.append(weighted_impurity)
best_split = impurities.index(min(impurities))
node["feature"] = values[best_split][0]
node["treshold"] = values[best_split][1]
The algorithm calculates all the possible splits and selects the threshold with the minimal weighted impurity to split the node.
6. Build the tree structure
def build_tree(train_X, train_y, node, max_depth, depth = 1):
# if the current depth is equal to max_depth, stop the splitting process
if depth < max_depth:
# find the best treshold and split the node
find_treshold(train_X, train_y, node)
node["left"], node["right"] = split_node(train_X, train_y, node, node["feature"], node["treshold"])
if node["left"]["leaf"] == False:
# re-execute this function with the left node as main node
build_tree(train_X, train_y, node["left"], max_depth, depth + 1)
if node["right"]["leaf"] == False:
# re-execute this function with the right node as main node
build_tree(train_X, train_y, node["right"], max_depth, depth + 1)
else:
node["leaf"] = True
This is a recursive function to build a tree based on a root node and a max_depth parameter.
7. Define the predict function
def predict(val_X, tree):
y = []
for index in range(len(val_X["LotArea"])):
current_node = tree
while not current_node["leaf"]:
# choose the path of the input samples
if val_X[current_node["feature"]][index] <= current_node["treshold"]:
current_node = current_node["left"]
else:
current_node = current_node["right"]
# predicted output is the mean value of the node where the input falls
y.append(current_node["mean_value"])
return y
This function locates the node where the input value falls in and returns the mean value of that node.
8. Fit a tree to the data
tree = create_node(y, [0, 1, 2])
build_tree(X, y, tree, 3),
print(tree)
> {'datapoints': [0, 1, 2], 'mean_value': 128.33333333333334, 'mean_variance': 1338.888888888889, 'leaf': False, 'feature': 'LotArea', 'treshold': 70, 'left': {'datapoints': [0, 1], 'mean_value': 102.5, 'mean_variance': 6.25, 'leaf': True, 'feature': None, 'treshold': None, 'left': None, 'right': None}, 'right': {'datapoints': [2], 'mean_value': 180.0, 'mean_variance': 0.0, 'leaf': True, 'feature': None, 'treshold': None, 'left': None, 'right': None}}
This is the written structure of a decision tree, just like the sklearn one. WE’VE DONE IT!
9. Predict unseen values
val_X = {
"LotArea" : [50, 90],
"Quality" : [7.5, 7.5]
}
print(predict(val_X, tree))
[102.5, 180.0]
Let’s go! These predictions make sense.
Decision tree from scratch full code
import numpy
X = {
"LotArea":[50, 70, 100],
"Quality":[8, 7.5, 9]
}
y = {
"SalePrice":[100, 105, 180]
}
def create_node(train_y, datapoints):
datapoints = datapoints
mean_value = numpy.mean([train_y["SalePrice"][y] for y in datapoints])
mean_variance = numpy.mean([(train_y["SalePrice"][y] - mean_value) ** 2 for y in datapoints])
leaf = False if mean_variance != 0 else True
return {
# datapoints index in the node
"datapoints" : datapoints,
# mean output value of the data points in the node
"mean_value" : mean_value,
# impurity of the node
"mean_variance" : mean_variance,
# leaf state
"leaf" : leaf,
# best feature and treshold to split the node
"feature" : None,
"treshold" : None,
# the left sub-node of the node
"left" : None,
# the right sub-node of the node
"right" : None
}
def split_node(train_X, train_y, node, feature, treshold):
node_left = create_node(train_y, [x for x in node["datapoints"] if train_X[feature][x] <= treshold])
node_right = create_node(train_y, [x for x in node["datapoints"] if train_X[feature][x] > treshold])
return node_left, node_right
def find_treshold(train_X, train_y, node):
values = []
impurities = []
for feature in train_X:
for treshold_index in node["datapoints"]:
node_left, node_right = split_node(train_X, train_y, node, feature, train_X[feature][treshold_index])
if len(node_left["datapoints"]) == 0 or len(node_right["datapoints"]) == 0:
continue
weighted_impurity = node_left["mean_variance"] * len(node_left["datapoints"]) / len(node["datapoints"]) + node_right["mean_variance"] * len(node_right["datapoints"]) / len(node["datapoints"])
values.append([feature, train_X[feature][treshold_index]])
impurities.append(weighted_impurity)
best_split = impurities.index(min(impurities))
node["feature"] = values[best_split][0]
node["treshold"] = values[best_split][1]
def build_tree(train_X, train_y, node, max_depth, depth = 1):
# if the current depth is equal to max_depth, stop the splitting process
if depth < max_depth:
# find the best treshold and split the node
find_treshold(train_X, train_y, node)
node["left"], node["right"] = split_node(train_X, train_y, node, node["feature"], node["treshold"])
if node["left"]["leaf"] == False:
# re-execute this function with the left node as main node
build_tree(train_X, train_y, node["left"], max_depth, depth + 1)
if node["right"]["leaf"] == False:
# re-execute this function with the right node as main node
build_tree(train_X, train_y, node["right"], max_depth, depth + 1)
else:
node["leaf"] = True
def predict(val_X, tree):
y = []
for index in range(len(val_X["LotArea"])):
current_node = tree
while not current_node["leaf"]:
# choose the path of the input samples
if val_X[current_node["feature"]][index] <= current_node["treshold"]:
current_node = current_node["left"]
else:
current_node = current_node["right"]
# predicted output is the mean value of the node where the input falls
y.append(current_node["mean_value"])
return y
tree = create_node(y, [0, 1, 2])
build_tree(X, y, tree, 2),
print(tree)
val_X = {
"LotArea" : [50, 90],
"Quality" : [7.5, 7.5]
}
print(predict(val_X, tree))